A couple days ago, my former colleague Sarah Mei trolled nerds everywhere, claiming programming is not math. In her post, she argues that the value proffered to a programmer by learning/knowing/doing math is greatly diminished compared to what widely held beliefs about math and programming would suggest. In particular, she claims that:
- Most developers don't require any applications of math in nearly all of the problems they need to solve.
- Understanding math-flavoured concepts from computer science, such as big O analysis, has little correlation with a solid understanding of the problems most developers need to solve.
- While programmers do require abstract thinking and problem solving skills, there is nothing special about math as a way to develop these skills.
So the question that's truly of interest here is not whether programming is math, but
In what ways, and to what extent, does learning and knowing math and computer science help programmers solve problems?
In fairness to Sarah, her post is indeed about this more interesting question, the title of her post is just clickbait. In fairness, so is the title of this post.
While I agree with some of Sarah's points, there are flaws in her arguments. I plan to critique some of those arguments, and then shed some light on the question of interest from my perspective as an almost-mathematician-turned-software-engineer. In this post, I'll address claim 1, and in Part 2 I'll address 2 and 3.
Applying math to solve programming problems
Sarah asserts that "the vast majority of developer jobs only required middle-school math at the most." There's a couple problems I see with this:
Biased Sample
Sarah does acknowledge the possibility she simply wasn't seeing the jobs that required more math than that, but doesn't take that possibility to its logical conclusion. And it's perfectly understandable. Sarah spent many years as a consultant, working predominantly with Rails and JavaScript, and teaching clients the Agile Way. Now she teaches Rails and JavaScript to newcomers.
If you have Rails, JavaScript, and Agile on your resume, and you're a relative novice to these things, you will be inundated with messages from recruiters+ at various companies who all need you to solve roughly the same class of problems, a class of problems that usually requires very little math. If you're as talented and experienced as Sarah, I can only imagine. What you will undoubtedly see is that there a ton of job openings like this that don't require much math. What that evidence does not bear out is the conclusion that the vast majority of jobs are like this.
What about finance, supply chain management, graphics, game engine programming, machine learning, and signal processing, just to name a few? In his response to Sarah's post, Jeremy Kun expounds on several of the "mind-bogglingly widespread applications of mathematics to industry." I recommend checking it out.
+Pro Tip: If you need a job, and don't mind working on the next Facebook/Pinterest/Instagram for dogs/seniors/snowboarders, then 1. Learn Rails and JS, 2. Profit.
Red Herring
Sarah talks about the math that is required for those jobs. Math may not be required for many jobs, but are there applications of math that allow you to solve problems in a better way than simply what's required? That's the real question. I'm going to get to a couple examples in just a second, but the gist is:
- The more math you know, the better.
- There will be occasions where you can get by without it, but where an application of math is the absolute best tool for the job at hand.
- Having math skills in your toolbelt gives you more options and approaches to solve whatever problem you might be faced with, be it design, debugging, experimentation, optimization, understanding someone else's code, etc.
- Whereas some areas of the tech industry need very little math, there's no dearth of tech jobs where strong math skills are a major asset.
I would liken it to knowing the power of raw SQL and how to roll your own queries vis-à-vis relying on an ORM for everything. Replace "math skills" with "roll your own SQL" in the statements above. The analogy is clear, with math simply being a bigger and more powerful set of skills than SQL.
Examples
WARNING: There is actual math below, with equations and this thing: ∑ k = 1N − 1, and bipartite graphs and Pascal's Triangle. If you wish to continue reading about the merits of math but don't want to look at any math just now, do not pass this link, go directly to Part 2: ☞
Otherwise, here's just a couple recent examples where I was working on implementing or testing a feature that had nothing to do with math, but was able to apply math to great effect.
Graph Theory and BDD Testing
This first example is about using pure graph theory to improve a BDD testing framework for Golang. Gomega is a matcher library which often used along with the Ginkgo testing framework. Gomega allows you to make assertions like:
1
| |
The ConsistOf matcher was recently added, allowing one to make assertions such as:
1 2 3 4 5 | |
It's useful when you want to say that some actual slice or array should look like some expected sequence of values, but the order doesn't matter. One of the features of this matcher is that it allows composition with other matchers. For instance, there's a ContainElement matcher which you can use like this:
1
| |
Now you can compose this with ConsistOf to make assertions like:
1 2 3 4 | |
The order of the sub-matchers shouldn't matter, so the following assertion should also pass:
1
| |
and indeed it did. The problem arose when you had an assertion like this:
1
| |
It should pass: x satisfies both sub-matchers, and y satisfies the first one. But it didn't. The problem is that the implementation of this matcher would look at the first sub-matcher, ContainElement(2), and find the first element in the given slice that satisfied it, x in this case. At that point, x is no-longer available. Then it tries to find a match for the next sub-matcher, ContainElement(1), and it only has one element to choose from, namely y. But y doesn't satisfy this, so it falsely reports a failure for the assertion.
What's the fix? Well, naively, you might consider going through every permutation of the input slice, and seeing if the ith element of the (permuted) slice satisfies the ith matcher. If, for some permutation, every element satisfies its corresponding matcher, then the assertion is marked as passing; else, it's a failure.
How bad is this approach? O(n!) -- really bad. Graph theory to the rescue! Thanks to this answer on cs.stackexchange.com, I was able to find the Hopkroft-Karp algorithm and apply it to this problem. It's runtime? O(n2. 5), not bad at all compared to the original O(n2) implementation, and, more importantly, no false negatives!
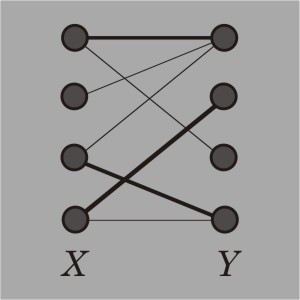
Source: https://www.mathworks.com/matlabcentral/fileexchange/screenshots/1307/original.jpg
Here's the idea. Model the problem as a bipartite graph, with the n elements of the actual array or slice on the left, and the n sub-matchers on the right. Do a pre-processing step of going through each pair of an element and a matcher (there's n2 such pairs), and connect the two vertices with an edge if that element satisfies that matcher. Then, use Hopkroft-Karp to do the hard work of determining if there is a way to choose exactly n edges so that each element on the left is paired with a unique matcher on the right, i.e. no two edges in this selection share a vertex. In the picture above, the bold edges represent an attempt to do this, except it was only able to find 3 edges. You can convince yourself that in that picture, there is a different way to choose 4 edges so that no two share a vertex, but not one that includes the 3 edges chosen so far.
Probability Theory and Load Balancers
I work on Cloud Foundry. It's a Platform-as-a-Service, so it let's SaaS developers push their source code, ask for n instances of the application to be run (in parallel, on separate servers), and then expose their app to their users on the web via a URL like my-app.my-domain.com, with the expectation that all traffic to that URL will be load-balanced across the n servers. I'm working on a team that's rewriting much of Cloud Foundry in Go. To test that our new code is working, we wanted to write a high-level system test which pushed an app, asked for 3 instances, and then make some requests to the app's URL and somehow assert that it eventually hit all 3 instances.
Now if the load balancer is doing its job and randomly but uniformly distributing load to all three servers, then there's some chance, albeit small, that even if you curl the endpoint 100 times, you'll never hit one of the app instances. In other words, even if the parts responsible for starting up 3 instances are working, and even if the parts responsible for keeping instances up and running (or restarting them quickly if they crash) are working, and even if the load balancer is being fair and balanced, there's some chance that you'll just happen to never hit one (or two) of those instances. A case like that would be a false negative.
So the question is, if I'm going to write a test that hits the app's endpoint in a for loop, how many times do I have to iterate to have 99.9% that I won't encounter a false negative. We want to be pretty sure that if this test ever fails in the future, it should be catching a real failure within the system.
The solution: let's solve for N, where N is the smallest integer where the probability of a false negative when hitting the endpoint N times at most 0.1%, or 0.001. Before reading further, take a guess as to what N might be. 5, 10, 100, 1000?
The probability of a false negative is equal to the number of ways a false negative can occur, divided by the total number of possible outcomes. Here, an "outcome" is a sequence of the N instance numbers hit when repeating the curl, e.g. if N = 14, one possible outcome is [1, 2, 2, 1, 1, 3, 3, 2, 1, 3, 2, 2, 1, 3]. Clearly, there are 3N total possible occurrences?
How many outcomes are false negatives? There's two kinds. The kind where you only ever hit one of the instances, so [1, 1, ...], [2, 2, ...], and [3, 3, ...]. There's just 3 of those. The other kind is where you only hit two of the three instances. So you either only hit 1 and 2, or only 2 and 3, or only 1 and 3. By symmetry, you can see that the number of outcomes for each of those three cases is the same, so let's just count one case and multiply by 3. How many ways to only hit 1 and 2? This means that you hit instance 1 somewhere between 1 and N − 1 times, and instance 2 the rest. Breaking it down further, for some k between 1 and N − 1, how many outcomes involve hitting 1 k times, and hitting instance 2 N − k times? It's easy to see that it's just ${N \choose k}$. So the inequality we want to solve is:
$\frac{3 + 3\sum_{k=1}^{N-1}{N \choose k}}{3^N} \leq 0.001$
Now here's something neat. We're almost looking at $\sum_{k=0}^{N}{N \choose k}$, which you might recognize is the sum of the Nth row in Pascal's Triangle. And that sum reduces to 2N because given a set of size N, the number of ways to choose a subset of size 0, plus the number of ways to choose a subset of size 1, ..., plus the number of ways to choose a subset of size N, is simply the total number of ways to choose a subset. And an equivalent way to choose a subset is to look at each element and make the binary choice "yes, you're in the subset" or "no, you're out", and there's 2N ways to do that. This kind of argument is called a combinatorial argument, where you prove two things are equal by showing that they represent two ways to count the same thing.
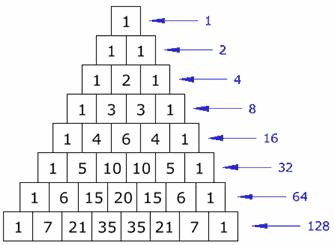
Source: https://www.mathsisfun.com/images/pascals-triangle-4.gif
An alternative argument uses the Binomial Theorem and the observation that (1 + 1)N = 2N. At any rate, we get:
$\frac{3 + 3\cdot(2^N - {N \choose 0} - {N \choose N})}{3^N} \leq 0.001$
$\frac{2^N - 1}{3^{N-1}} \leq 0.001$
N = 20
And that's indeed what we do. We poll 20 times, and then assert that we see all 3 instances. By the way, did you guess 20?
Before we move on, here's a question: what if we have more than 3 instances? Let's just say 4. The problem already gets way harder. The Pascal's Triangle trick no longer applies. How do you model the problem now? Well, here's one approach, and the pretty results:
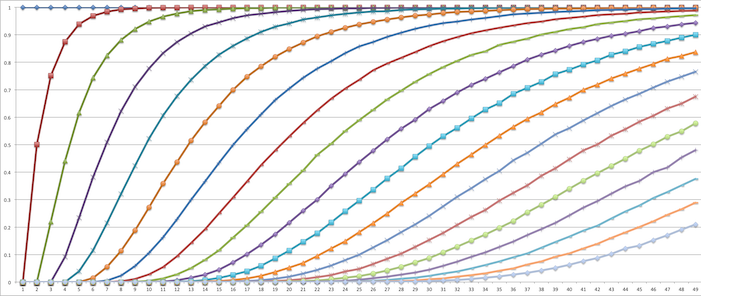
Now let's move on to Part 2.